置信区间是指由样本统计量所构造的总体参数的估计区间。在统计学中,一个概率样本的置信区间是对这个样本的某个总体参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度,其给出的是被测量参数的测量值的可信程度,即前面所要求的“一个概率”。
为了进一步说明,看一个例子。
一家食品生产企业以生产袋装食品为主,为对食品质量进行监测,企业质检部门经常要进行抽检,以分析每袋重量是否符合要求。现从某天生产的一批食品中随机抽取了25袋,测得每袋重量如下表所示。已知产品重量的分布服从正态分布,且总体标准差为10g。试估计该批产品平均重量的置信区间,置信水平为95%。
解答如下:

要看懂这个解答,我们需先知道:
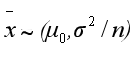
所以可以通过使用正态分布统计量 z:
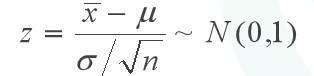
图一
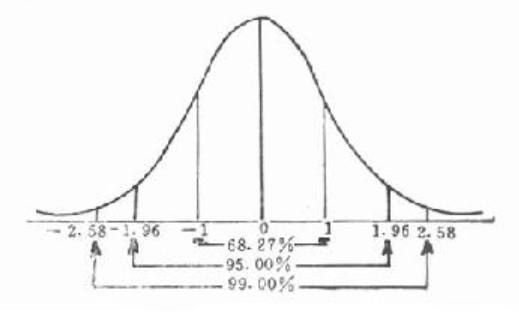
标准正态分布曲线
本问题中的置信水平为95%就意味着:
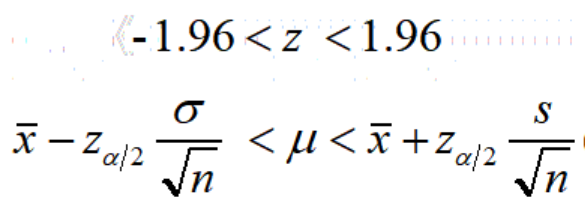
图三
上图中的两个不等式是完全等价的,而第二个不等式的计算结果正是本问题的置信区间:101.44g~109.28g。
那么,整个问题的提出和解决,如何进行描述呢?
一家工厂,想要知道自己生产的所有袋装食品的平均重量(总体均值),但又不可能每一袋都去称一下(成本太高),所以采取抽样的办法。而样品的平均值又不能直接作为全部产品的平均重量,所以通过将样品的平均值转换为标准正态分布后,再根据置信度的要求,得到一个置信区间,那么这个区间包含总体均值的可能性就是那个置信度95%。
也就是说,这个问题的本质就是用样本均值去估计总体均值,每次抽样以后,都可以由样本的平均值,按照置信度的要求,得到一个置信区间,而这个区间包含总体均值的可能性刚好就是置信度。
假设置信度为95%,也就意味着,如果抽样100次,那就可以得到100个置信区间,那么里面至少有95个置信区间包含总体均值。

 手机版
手机版