00、背景
比如,要考核一个研发人员,存在多个维度的评价指标,如:交付效率(需求交付周期、开发交付周期、交付吞吐量)、交付质量(线上缺陷密度 、故障恢复时间、首次提测通过率、单元测试覆盖率、代码评审通过率)、交付能力、360度反馈等多个维度。那么多维度的数据,该如何计算呢?
降维技术提供了一种方法,它捕获数据中的基本信息,同时丢弃冗余或信息较少的特征。
数据降维,至少有以下几点好处:
- 使数据集易使用
- 降低算法计算开销
- 去除噪声
- 结果易懂
- 发现隐性相关变量
降维主要实现技术有很多,比如主成分分析(PCA)、线性判别分析(LDA)、奇异值分解(SVD)、因子分析(FA)和独立成分分析(ICA)。
其中,PCA 的应用目前最为广泛。
01、什么是PCA?
PCA = 主成分分析(Principal Component Analysis)
PCA是一种数学降维方法, 利用正交变换 (orthogonal transformation)把一系列可能线性相关的变量转换为一组线性不相关的新变量,也称为主成分,从而利用新变量在更小的维度下展示数据的特征。
简单来说,就是找出一个或几个最主要的特征,然后进行分析。
注意:
降维是通过减少数据中的指标以化简数据的过程。
这里的减少指标,并不是随意加减,而是用复杂的数理知识,得到几个"综合指标"来代表整个数据。
而这里的综合指标就是所谓的主成分。
它不是原来的指标中的任何一个,而是由所有原有指标数据线性组合而来。
02、实现步骤
将数据转换为N个主成分的步骤:
- 去除平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值和特征向量
- 将特征值从小到大排序,保留前N个
- 5. 将数据转换到这N个特征向量构建的新空间中
03、优缺点及适用场景
优点降低数据复杂性,识别多个特征缺点可能损失有用信息适用场景数值型数据
04、举例
1、一个简单的测试数据集
1.1 原始数据文件testSet.txt,19K
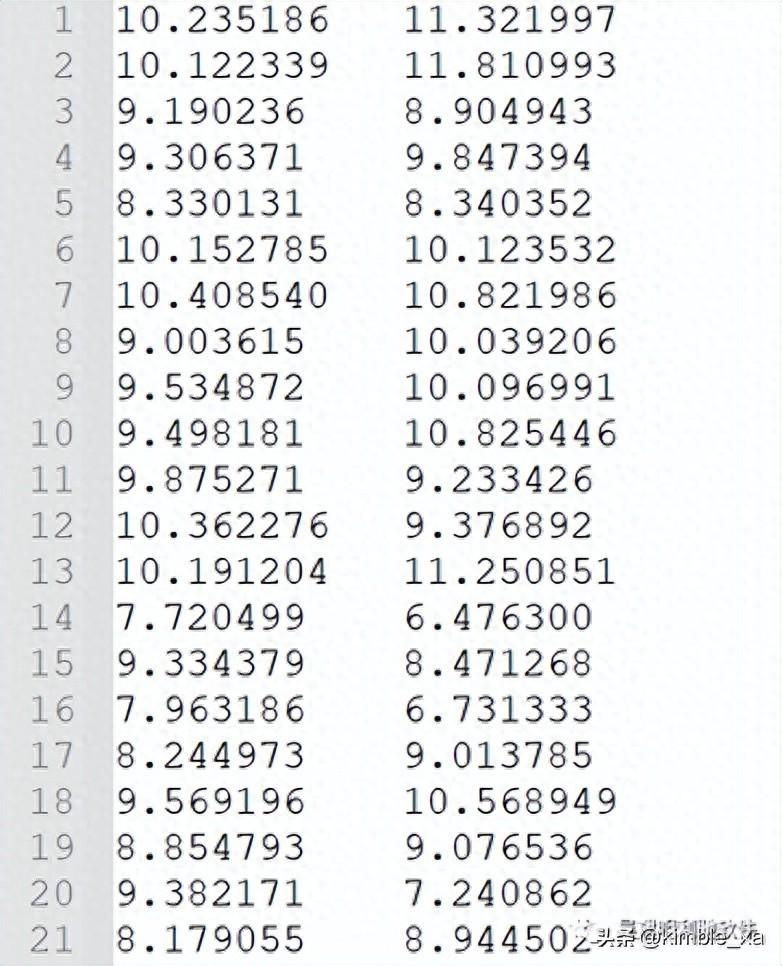
1.2 打印矩阵长度
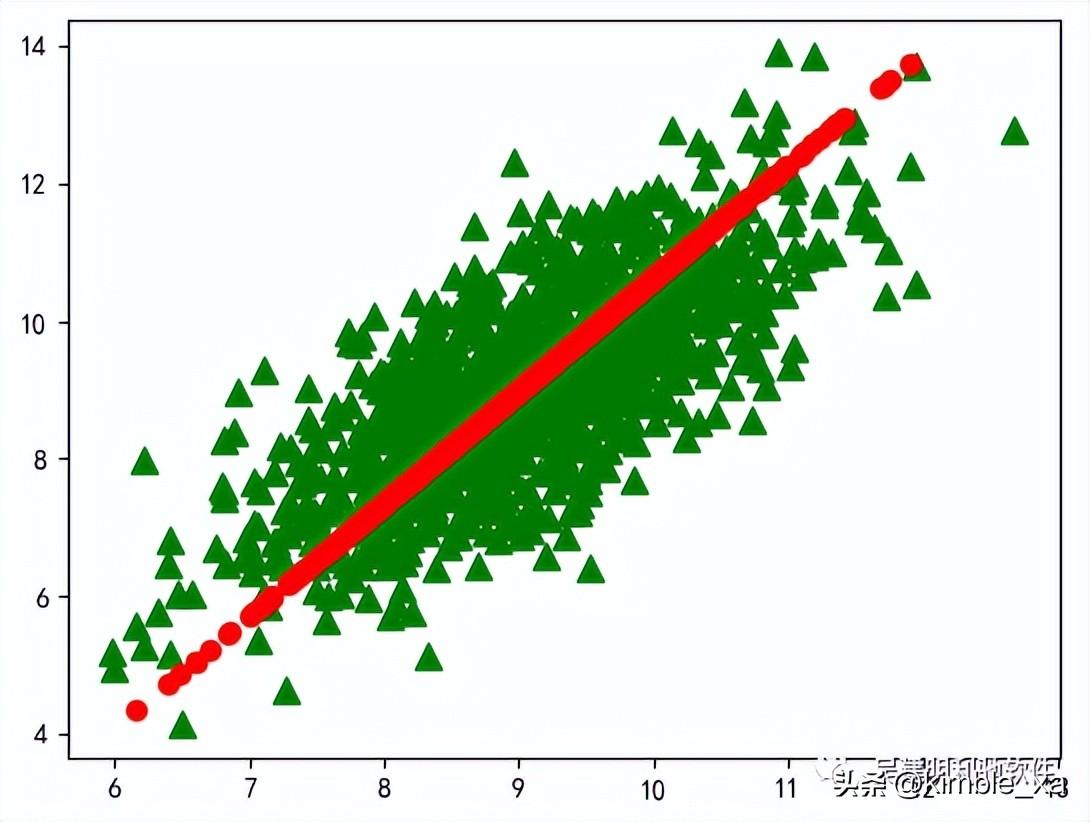
1.3 效果图
2、另一个半导体制造数据集
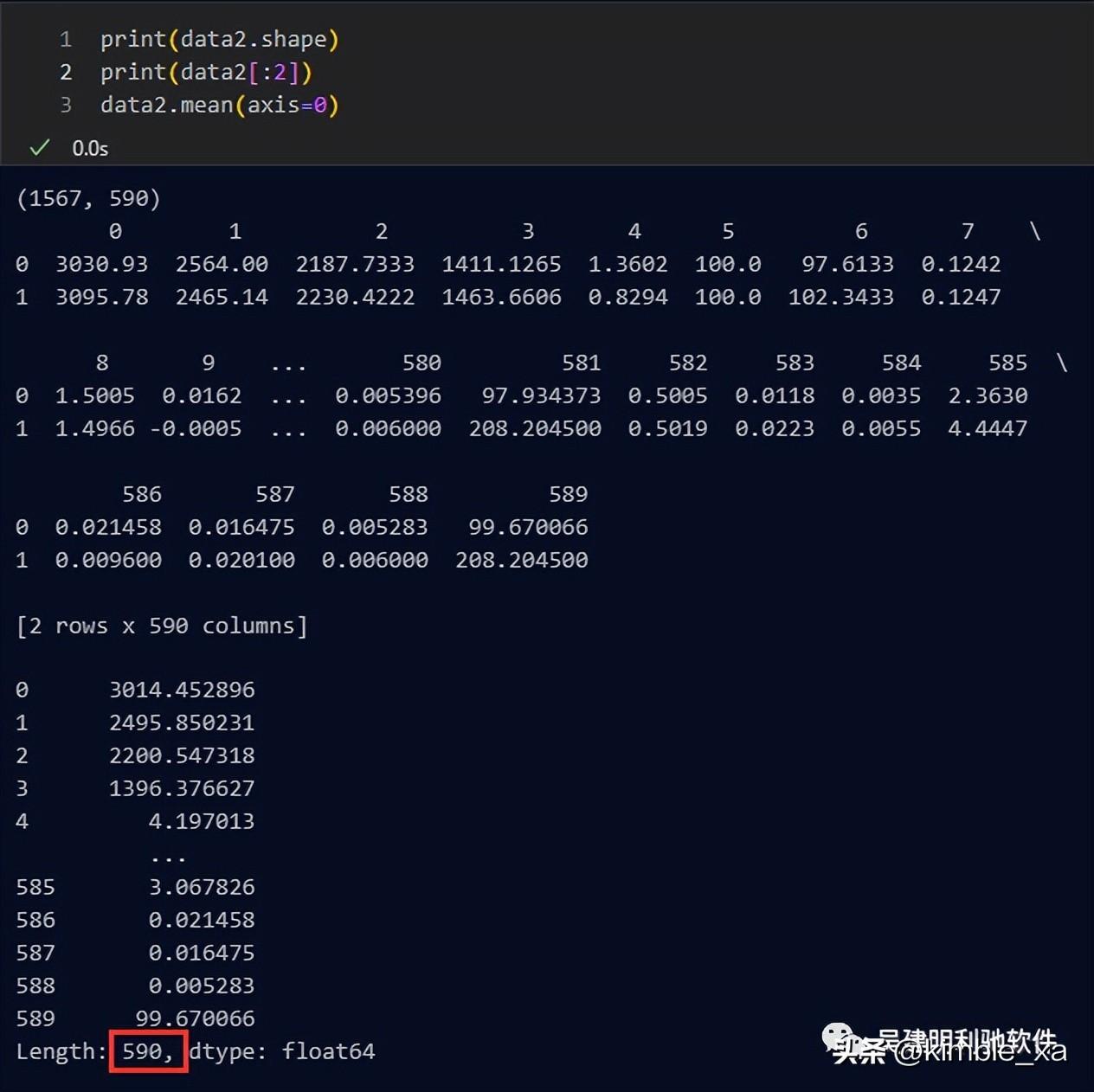
2.1 原始数据:共1567行数据,有590列维度

2.2 打印矩阵长度、数据及均值
2.3 画出方差变化与特征个数的关系图
2.4 得出结论
从方差百分比与主成分个数之间的关系可以看出,大概只需要6个特征,就可以包括大部分的方差,后面的成分并不会损失太多信息。如果保留前6个主成分,则数据集就实现了从590个特征简化到6个特征,实现了近100:1的压缩。
3、完整代码
'''
Author: wujianming
Date: 2023-10-18
'''
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
def loadData(filename,delim='\t'):
fr=open(filename)
stringArr=[line.strip().split(delim) for line in fr.readlines()]
dataArr=[list(map(float,line)) for line in stringArr]
return np.array(dataArr)
# 主成分分析
def pca(dataArr,topN=9999999):
"""
dataArr为数据集
topN参数可选,表示应用的N个特征,
或原数据中全部特征
"""
meanVal=np.mean(dataArr,axis=0)
newArr=dataArr-meanVal
# 协方差矩阵
covMat=np.cov(np.mat(newArr),rowvar=0)
eigVal,eigVec=np.linalg.eig(np.mat(covMat))
index=np.argsort(eigVal)
index=index[:-(topN+1):-1]
vecArr=eigVec[:,index]
lowDataMat=np.mat(newArr)*vecArr
retDataArr=(lowDataMat*vecArr.T)+meanVal
return lowDataMat,retDataArr
def load_clear_Data():
import pandas as pd
data=pd.read_csv('./secom.data',sep=' ',header=None,index_col=None)
for i in range(data.shape[1]):
data[i]=data[i].fillna(data[i].mean(),)
dataArr=np.array(data)
return dataArr
def plot_var(dataMat):
meanVals = np.mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals
covMat = np.cov(meanRemoved, rowvar=0)
eigVals,eigVects = np.linalg.eig(np.mat(covMat))
eigValInd = np.argsort(eigVals)
eigValInd = eigValInd[::-1]
sortedEigVals = eigVals[eigValInd]
total = np.sum(sortedEigVals)
varPercentage = sortedEigVals/total*100
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('主成分个数')
plt.ylabel('方差百分比')
plt.show()
def plot_data(dataArr,reconMat):
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(dataArr[:,0],dataArr[:,1],marker='^',s=90,c='b')
ax.scatter(np.array(reconMat[:,0]),np.array(reconMat[:,1]),marker='o',s=50,c='r')
plt.show()
if __name__=='__main__':
dataArr=loadData('./testSet.txt')
lowData,reconMat=pca(dataArr,1)
plot_data(dataArr,reconMat)
dataArr2=load_clear_Data()
plot_var(dataArr2)05、小结
为什么主成分可以代表原来那么多的指标呢?
其实我们仔细看一下,原来的许多指标是有相关性的,比如线上缺陷密度与单元测试覆盖率、代码评审通过率等有关联性。
通过降维就可以帮助我们去除这些指标中重叠、多余的信息,把数据最本质和关键的信息提取出来。

 手机版
手机版